Polytopes and how to make them regular17.VIII.2024
and why three and four-dimensional spaces are so cool
So, regular polytopes, huh. These have been one of my interests for quite a while now. Cute, elegant, and symmetric, they for some reason only exist in very small numbers (plus a couple infinite families, but more on that later). It's like they were made to be listed, collected and obsessed over, drawn, modeled, printed, painted; to be used as symbols for fundamental things (hi, Plato!). And i've done my fair share of most of these - and now will try to piece together my thoughts and proceedings on these shapes.
So what is a regular polytope? One might be inclined to think that's it's one of these good boys:

boop
and such an answer, though right, would be incomplete for the purposes of this silly review. Yes, you're looking at regular polyhedra in three-dimensional euclidian space. But what about two dimensions? Five? Sixty-nine? And how have we got here anyway?
..let's start from scratch here.

This will be our scratch: a line segment. Let's make it the one and only one-dimensional polytope by definition (and say it's regular by definition). The points at the ends - the two vertices - will be its border. When we say "one-dimensional", we mean that any point on can be fully described with just one coordinate (say, distance from one of the ends). Let's add another.
Setting a flat foundation
A two-dimensional polytope is called a polygon and, well, you probably know how to construct it: just throw a bunch of line segments on a plane...

...not like that, silly!
We want a polygon to be made of line segments (its edges), sure. But we also want to chain them together, sharing each and every vertice between two edges. This way, if we hop on any line and go along it, we might experience all sorts of turns and corners, but never a fork or a dead end. Thus it won't have any "border" points. Okay?

...oh stars.
See, that's why making a good mathematical definition is important. If we don't weed stuff like this from counting as polygons, we'll be having a lot of unexpected cases down the line. On one hand, why not. On the other... if we want to be able to adequately look at, touch and use our pretty shapes, it would help if they were less janky and more... makeable in the real world. So let's impose some restrictions.
First of, we want a shape to be connected. Two triangles weirdly floating near each other aren't a polygon, it's two polygons. Secondly, please, let's restrict our shapes to have a finite number of vertices, a zigzag line going into infinity on both ends isn't a polygon we can easily make. And finally: no intersecting segments. We already decided against forks in the road, this is just another cheeky way to make them.
Are we clear?

Thank the stars. Now it's time to generalize what we did so we can extend the notion into higher dimensions.
We took a finite amount of n-dimensional polytopes, n being 1; arranged them in (n+1)-dimensional space (on a plane); stitched them together two at each (n-1)-dimensional border (vertex); made sure there are no dead ends and no intersections. And got a (n+1)-dimensional polytope. Well, let's continue.
What will be our new border where we join things? Obviously, the edges. And what would be our new "insides" which should not intersect? Well, about that...
Yes, it is kind of obvious that what we just drew divides the plane in two parts. Yes, it's kinda obvious which one is the inside. But try stating that in 74-dimensional space and you've got yourself a problem. Thankfully, as we soon will see, this problem solves itself without needing to go into lengthy proofs - as, as soon as we start adding regularity to our polytopes, they will immediately all become convex. Not by definition, just as a lucky coincidence.
What is convex, you might ask? Let's take our polygon and draw a line through one of its edges. If the entire polygon falls on one side of it, good! If this holds for every edge, we got ourself a convex polygon. Now let's only keep the points of the plane which fall on the same side as the polygon regardless of which line we draw. That happens to be our inside. For higher dimensions just substitute lines with linear spaces - planes, etc.

At long last, the procedure is fully repeatable. Join segments two to a vertex, they become edges of a new polygon. Join polygons two to an edge, they become faces to a new polyhedron. Join polyhedra two to a face, they become cells to a new polychoron. Join polychora two to a cell... well, it appears we have run out of smart-sounding words, but this can be literally continued forever. Want to imagine a polytope in 196,882-dimensionsional space? You sure can try, just beware of monsters beyond your imagination.
But what is a regular polytope?
You remember the purpose of this was to get some pretty shapes, right? Well, pretty shapes are usually symmetric, so let's dump as much symmetry in as we can.
Line segments: perfect as they are, you can't really do anything about them. Polygons though... Well, symmetry kindly asks me to make all edges the same (they are segments so same length will do). This still leaves wiggle room for stuff like this:

...so let's also ask the shape to look the same at each vertex. To do it the formal, useful-later and easily generalizable to however-many-dimensions way, let's define it like that: pick a small distance, pick a vertex, place a dot that distance from each vertex at each edge, connect the dots. Congratulations! You just made a set of vertex figures, and these are the things which, just like the edges, should all be the same. Aren't they pretty?

Yes, for now they are just lines. And yes, for now them being the same is equivalent to all angles being the same. But if we go that route, we'll have to measure angles between planes, then hyperplanes, then hyperspaces, and that's an awful lot of trigonometry. Trigonometry is hard. Comparing cute shapes is easy. Besides, there's a whole lot of additional symmetry hidden within these shapes - as soon as we leave the confines of the 2D plane. Which we'll do soon. I promise.
So what do we have now? All edges the same, all angles the same - and we suddenly lost the infinite freedom of moving points however we want. As soon as we determine the length and the angle, each next point's location is already predetermined. So these are the only two things we can change. How big the polygon is (symmetry whispers that size doesn't matter) as well as how pointy. Given that we should eventually somehow close the loop and not self-intersect in the process, even the angle falls on a spectrum of discrete values. Entirely determined by the amount of vertices we place before closing the loop.

hey there cuties!
Thank the stars! We just listed all regular 2-dimensional polytopes! And all of them sure are hella convex!
Well, not all of them. But the pattern obviously continues: these guys form an infinite family. And that's exactly why 2D, though a useful building block, is not as interesting as what awaits us ahead. Sure, a regular 65,535-sided polygon is technically different from a 65,537-sided one, but if you looked at them from a distance, you would just see two circles. And as cute as looking at circles might be, it's not that riveting past the 65,535-th one.
Take a small break. Relax. Drink some water (for the water god). Look at pretty circles. And when you're ready to join me, proceed.
Onwards to 3D!
Fiddling around in space
Let's reiterate our components for building our regular 3D polytopes - regular polyhedra. We know what a polyhedron is, we went through it together. We know a regular polygon: all edges the same, all vertex figures the same. Now let's ask our polyhedron to adhere to a similar standard: all faces the same, all vertex figures the same. Oh, and while we're at it, let's also ask them to be regular polytopes themselves. This is something which did itself automatically on the plane - when they were just segments, and all segments we defined as regular - but now, and in all subsequent dimensions, we need to keep track of this as well. This makes the notion of regular polytopes expandable into any dimension via a bunch of self-referencing. After all, pretty shapes have to have pretty faces, right?
And here's where the magic comes in. We want our faces and vertex figures to be regular polygons. But we already found all of these! So we can just pick two from the list - and the rest is done for us. We'll just sit and watch the resulting shape being built before our eyes.
Except not any two will do. At least, as long as we're working in euclidian space. It has a property that somewhat restricts our freedom: when we meet several shapes all around a vertex on a plane, their angles always sum up to the same amount (defined as 360 degrees). And when we do that in 3D space... well, we can technically exceed it, but not without losing our regular-polygon vertex figure. Here's why:
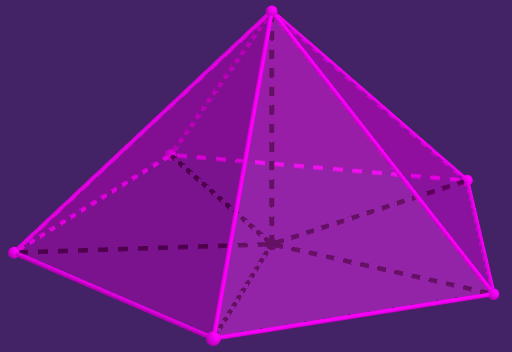
With all sides the same regular polygons, we have to arrange them around a vertex in this all-around-symmetrical pyramid (its bottom face being the vertex figure). Let's now project the vertex and edges onto this figure. All the angles can only get bigger this way - and on the plane the sum is 360. Meaning that above the plane it's bound to be less.
If you are disappointed by that restriction, you might like hyperbolic space. I quite like it myself, it's fun and trippy. Our space, however, is not hyperbolic (at least, at scales and under conditions typical for human life). As such, we shall schedule a trip to hyperbolic space to some other day - and try to make sense of what our friend Euclid left us with.
A regular polygon for a side, a regular polygon for a vertex. The pair determines what polyhedron we get, if any. And since polygons themselves are completely determined by the number of their vertices, let's write down the combinations as number pairs. And go through them in ascending order.

careful now, don't step on this
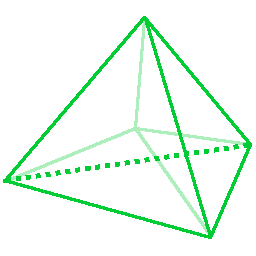
• (3, 3) - anything less then 3 doesn't have an associated polygon, so we start here. Three triangles meeting at each vertex: hello, tetrahedron. Neat little shape - four vertices, six edges, four sides. It's the only spiky one in 3D - it has vertices opposite to sides, all others have sides to sides. I find this property of it quite tasty. Also look what it can do!

If we join the middles of each face together, we get another tetrahedron. This operation is called making a dual polytope. Each face is now a vertex, and each vertex is now a face - (a, b) becomes (b, a). Though it's not exactly like making vertex figures - back then we were placing points on edges, not faces - the result is the same. In higher dimensions, vertex figures of a polytope and faces of its dual will themselves be dual polytopes of one dimension lower, but now we're working with polygons, and regular polygons are all self-duals. In any case, a dual figure for a regular polytope gets a regular face and a regular vertex figure, thus is a regular polytope itself. Tetrahedra are dual with themselves, but this isn't the case for our next two.

• (3, 4) - four triangles around a vertex: octahedron. (4, 3) - three squares around a vertex: cube. Triangular antiprism and square prism. Both manifest three perpendicular axes of 3D space: for the cube it's in edges, for the octahedron - in pairs of opposing vertices. Six vertices, twelve edges, eight sides; six sides, twelve edges, eight vertices.

and they are, in fact, duals to one another

• (3, 5) - five triangles around a vertex: icosahedron. (5, 3) - three pentagons around a vertex: dodecahedron. These two are also duals to one another and are quite a complicated sight (12/20 vertices/faces, 30 edges) - this complexity is nothing compared to their 4D-counterparts, though.
(3, 6), (4, 4) and (6, 3) bump right into that 360 degree barrier - and instead of folding into a polyhedron, tile the plane:

which - as we outlawed having infinitely many vertices! - doesn't count. And everything past that goes right over 360. Our 3D collection is as such complete.
Quite a different story compared to the infinite family in 2D. And yet these few, these five are meaningful. And beautiful. And as we'll soon see, 4D will give us even more wonders. Drink some water and let's go a step further.
Miandering in hyperspace
Before we begin, let's lay some additional foundation.
It may be tempting to start behaving like in 3D, grabbing all possible pairs of faces and vertex figures from the dimension before and combining them. In fact, we only had 5 regular polyhedra, so there's only 25 possible combinations.
Well... you may try. If you're verse with hyperspace (if you dared to try, i expect you are), you'll soon notice the problem. Vertex figures are now 3D polyhedra, and so are faces (called cells). And if you look closely, you'll notice an interesting relation between them: face polygons of a vertex polyhedron are exactly vertex polygons of a face polyhedron!

here, 4 cell tetrahedra are meeting at a vertex, sharing 4 edges. the vertex figure is another tetrahedron; each face of this tetrahedron is also a vertex figure of one of the cell tetrahedra by definition.
Thus, a face polyhedron (a, b) - its vertex polygon b-sided - can only be paired with a vertex polyhedron (b, c) - made of b-sided polygons. It is logical to denote that potential polychoron as (a, b, c). And this follows into further dimensions! An (a, b, c) face polychoron would only be able to pair with a (b, c, d) vertex polychoron, and so on.
This further limits the amount of polychorons to check - to the following lists: (3, 3, 3), (3, 3, 4), (4, 3, 3), (3, 4, 3), (4, 3, 4), (3, 3, 5), (5, 3, 3), (3, 5, 3), (5, 3, 5). Let's check. Also a quick note: as polychora aren't as popular of a topic as polyhedra, there's like a dozen alternative names for each, i only will list those i like most.
We can also note from the picture above that the edge in a polychoron (a, b, c) is shared by the same amount of (a, b) polyhedra as there are faces sharing a vertex in the (b, c) vertex polyhedron - so by c polyhedra. This will also follow into larger dimensions: an (a, b, ... w, x, y, z) n-dimemsional polytope has z copies of (a, b, ... w, x, y) - its (n-1)D faces - around an (a, b, ... w) - an (n-3)D face of a face of a face.
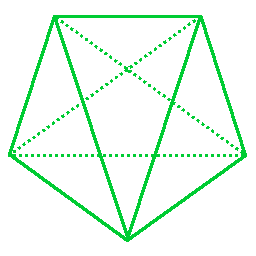
• (3, 3, 3) - pentachoron. 5 vertices, 10 edges, 10 triangles, 5 tetrahedra. You have already seen it just one picture earlier! It's really quite simple for a polytope. Similarily to a tetrahedron, it is self-dual. And we can already note that triangle, tetrahedron and pentachoron are a start of an infinite family of the form (3, 3, ... 3) - each next n-polytope being the same as the last, plus one additional vertex raised into the new dimension - providing n more copies of the last one. These guys are named simplexes.
Yes, it also secretly looks like a pentagram from a certain angle! Projections in general can change the visual feel of a polychoron quite a lot! For this and two next polychora i have included two projections for each: the first one to make the structure of the polychoron more obvious, and the second one - the most cool-looking in my opinion.


• (3, 3, 4) - orthoplex. 8 vertices, 24 edges, 32 triangles, 16 tetrahedra. Strictly speaking, orthoplex is a family name of yet another infinite family of (3, ... 3, 4) - now each next dimension we add two more poits, not one, and pull them to both sides of the previous hyperplane. Our 4-orthoplex descends from an octahedron in this way.

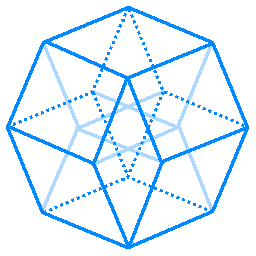
• (4, 3, 3) - hypercube or tesseract. 16 vertices, 32 edges, 24 squares, 8 cubes. I'm sure this one is the best known. Is in one family with a square and a cube: now each next dimension we copy the whole previous shape up, connecting the copied vertices with originals (and doubling their amount each time). This family of (4, 3, ... 3)-type polytopes are just known as n-cubes and are used in defining higher-dimensional analogs of volume. Yes, orthoplex and hypercube are duals; duals in high dimensions reverse the whole (a, b, ... x) sequence to (x, ... a, b).
It took me longer than i'd like to admit to find a cool projection for the hypercube, but i found one! Yes, all the cubes got askew, but all sets of parallel lines remain parallel. If you plop it all the way into 2D, you'll get pretty eight-rayed stars, but if you don't - there's a rhombic dodecahedron in there, how about that? :D

• (3, 4, 3) - octacube. 24 vertices, 96 edges, 96 triangles, 24 octahedra. This one is very unique: nothing like this occurs in any other dimensionality (the closest analogue being a 3D cuboctahedron, but it's not a regular polyhedron). And as such, it is my favorite! Also it has a cuboctahedron in a middle crossection between two parallel octahedra, which can be seen on the picture if you look closely :3

• (4, 3, 4) - cubes 4 to an edge, and they tile 3D space. Not a polychoron.

• (3, 3, 5) - tetraplex. I worked quite a bit on this one trying to figure out all the different connections! It has 120 vertices, 720 edges, 1200 triangles and 600 tetrahedra. Technically i drew only half a tetraplex here. As its cross-sections, it has an icosidodecahedron in the middle (w = 0) - you can see it as the outer shell of the drawing - then an icosahedron at w = 1/2φ (but only the vertices, without edges connecting them), a dodecahedron at w = 1/2, another icosahedron (this time with edges) at w = φ/2 and a vertex at the pole (w = 1). The same goes in the other (w < 0) direction.

• (5, 3, 3) - dodecaplex. 600 vertices, 1200 edges, 720 pentagons, 120 dodecahedra - i had to code this one to even draw it, and even then it's also only a half, but the result is worth it! It's soooo bubbly!~ (and yes it's obviously dual with the tetraplex why even ask)
(3, 5, 3) - three icosahedra around a vertex - do not fit, neither do (5, 3, 5) - five dodecahedra around a vertex. And that's it.
Holy mother of goats - we're done! It took me literal hours to make the last two, but we're done with 4D!
And let me tell you. 4D polychora are beautiful! They're way more complex and symmetric than polyhedra, especially these last two ones. And the dodecaplex in particular is rumored to contain in itself subsets of vertices which form all the other regular polychora and polyhedra - how about that? :D My favorite's still the octacube, though. It's way easier to draw.
I would make a break here. I probably should make a break here. But honestly, there's so little interesting beyond this point that i probably can do the rest quite quickly.
Ever-transcending sequences
Welcome to 5D and... oops.
There's not too much to do here. We have six polychora to work with, and a quick check only leaves us with these viable combinations to check for being a 5-polytope: (3, 3, 3, 3); (4, 3, 3, 3); (3, 3, 3, 4); (4, 3, 3, 4); (5, 3, 3, 3); (3, 3, 3, 5); (5, 3, 3, 5).
We already know three of these. We met their families before. (3, 3, 3, 3) is a 5-simplex, (3, 3, 3, 4) is a 5-orthoplex, and (4, 3, 3, 3) is a 5-cube. (4, 3, 3, 4) tiles 4D space with infinite hypercubes (trippy!). (5, 3, 3, 3) - three dodecaplexes around a pentagon - as mind-blowing as this shape could've been, it doesn't exist: they don't fit. Five of them, obviously, don't fit even more (for 5, 3, 3, 5), neither do five pentachora (for 3, 3, 3, 5). This removes the number 5 from the board outright. So 5D has only three regular polytopes.
And as we continue, the pattern repeats itself. We always have an n-simplex, n-orthoplex, n-cube; we also get an (n-1)-cubic tiling on each step, which doesn't count. And we never get anything else. This holds for all the following spaces eternally and forever. That's it.
On one hand, it's kind of sad. On the other, thank the stars i don't have to draw a five-dimensional dodecahedron metaphor with like six million vertices or something, because it doesn't even exist. And it's kind of nice to have a concluding, all-encompassing, ultimate shape like the dodecaplex.